Reflection
To begin this project, we started out with the activity of Game of Pig. The game is a two dice probability game that can be used to understand how probability can affect us in places that we wouldn't expect to see probability. Since you are rolling a die many times in one turn, you follow different paths on a imaginary probability tree diagram, you might roll a 4,5,2 and 3 but it will all be taken back if you roll a 1 in the same turn. This is where the probability and strategy comes in; while playing you can test out strategies to have optimal scores per turn without canceling them out by rolling a 1. This activity was done to open our minds to the idea that probability is in many things that we do and to teach us that there is a way to determine the likelihood of something, by studying probability.
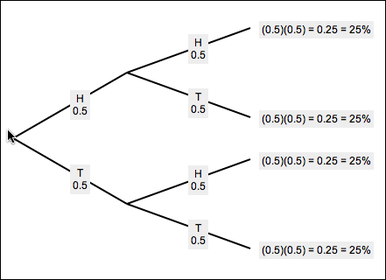
We then started to experiment more with what probability is and its extent of control over games and other events. We learned about Observed probability when doing the Waiting on a Double and Gambler's Fallacy activities. These activities required us to record the amount of rolls it took to get a double when using two dice or how often you could get three heads in a row when flipping a coin 25 times. We then compiled the data from some of these observed probability activities into individual frequency bar graphs and we compared them to the class data set. We learned about Theoretical probability to help us understand why Observed probability can be useful. By determining the Theoretical probability, which is the number of outcome that we are interested in over the total number of outcomes, we have a mathematical basis of what the outcomes should look like. By increasing the data of our observed probability, it gets closer and closer to the theoretical probability, this is because the larger number of data in observed results gives a more stable curve that is normally achieved with theoretical probability.
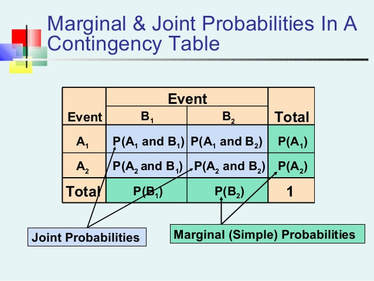
Once we understood how we could take different events and organize the data, we started to get more complex by learning about conditional probability. With conditional probability came many useful tools such as Probability Trees and Two Way Tables. Probability trees helped us map out the outcomes of events, this was especially useful when you needed to see how the probabilities changed or how you could get to a final outcome. Two way Tables were another organizational skill that helped me compile the data into one table for easier managing. This tool was useful alongside probability trees because it took all of the information on the tree and further organized it in a way that showed the totals in the form of marginal probabilities (the probabilities of only one event happening ). The inside of the two way tables showed the joint probabilities or the probabilities that one thing from event A and one thing from event B happened. This table was a great way to learn about why and how the two forms of probabilities existed as well as staying organized when we had big amounts of data to analyse.
We then started to experiment more with what probability is and its extent of control over games and other events. We learned about Observed probability when doing the Waiting on a Double and Gambler's Fallacy activities. These activities required us to record the amount of rolls it took to get a double when using two dice or how often you could get three heads in a row when flipping a coin 25 times. We then compiled the data from some of these observed probability activities into individual frequency bar graphs and we compared them to the class data set. We learned about Theoretical probability to help us understand why Observed probability can be useful. By determining the Theoretical probability, which is the number of outcome that we are interested in over the total number of outcomes, we have a mathematical basis of what the outcomes should look like. By increasing the data of our observed probability, it gets closer and closer to the theoretical probability, this is because the larger number of data in observed results gives a more stable curve that is normally achieved with theoretical probability.
Once we understood how we could take different events and organize the data, we started to get more complex by learning about conditional probability. With conditional probability came many useful tools such as Probability Trees and Two Way Tables. Probability trees helped us map out the outcomes of events, this was especially useful when you needed to see how the probabilities changed or how you could get to a final outcome. Two way Tables were another organizational skill that helped me compile the data into one table for easier managing. This tool was useful alongside probability trees because it took all of the information on the tree and further organized it in a way that showed the totals in the form of marginal probabilities (the probabilities of only one event happening ). The inside of the two way tables showed the joint probabilities or the probabilities that one thing from event A and one thing from event B happened. This table was a great way to learn about why and how the two forms of probabilities existed as well as staying organized when we had big amounts of data to analyse.
These tools helped us visualize the events that took place but also made it easier to identify when an event occurred given that a previous event occurred. For example if you had a bag of 6 marbles, three red and three green, and you took one red marble out, the chance that the next marble that you take out is red given that the previous marble is also red is 2/5. Something that helped put everything into context was determining if an event was dependent or independent. If the event was completely separate from the event before or after it in terms of influence on the outcome, it would be independent. If it did contribute to the probability of the other event, however, it would be dependent.
another aspect of probability analysis that deals with multiple probabilities is the probability of multiple events. This is when you are looking for the probability of something or another thing occurring. For example if you roll die, what is the probability that you get a 3 or a 6? You would just add up the probabilities of the two to get the probability [3 or 4]. However, if there is an overlapping probability such as the probability that you get a 6 or an even number, you still add up the two probabilities but you subtract the probability of getting both a 6 and an even ( P[6]+P[even]-P[6 and even] ).
another aspect of probability analysis that deals with multiple probabilities is the probability of multiple events. This is when you are looking for the probability of something or another thing occurring. For example if you roll die, what is the probability that you get a 3 or a 6? You would just add up the probabilities of the two to get the probability [3 or 4]. However, if there is an overlapping probability such as the probability that you get a 6 or an even number, you still add up the two probabilities but you subtract the probability of getting both a 6 and an even ( P[6]+P[even]-P[6 and even] ).
Another portion of this project was to apply all that we learned by recreating a game of chance from the renaissance and analyzing how probability took a role in determining your fate in the game. We started research on games as soon as we started our work with probability. We had many resources such as www.modaruniversity.org/Games.htm and www.tradgames.org.uk/ as well as other cross reference and information sources like the Encyclopedia Britannica to research and determine which games would best fit our probability topics while also being engaging and fun to play. It was hard to research some games because of how little information there was on it but for the most part we could find information about the games to better understand how they were played and where they were played. The game that we chose to recreate was a game called Hazard. It was a game from the 13th century with an unknown origin (speculated to be Arab in origin because of the names similarity to the Arabic word for dice. It was mainly played in England but was popular around Europe as well. The game Craps derived from Hazard and that helped us understand and contrast the two games to see the similarities and differences. We chose this game because we thought it would be something that was easy yet entertaining for any audiences that might be playing it. The game is a two dice game that is played by first having the first player or caster establish a main by rolling the dice until getting a number somewhere between 5 and 9, then other players make a bet on whether the caster will get their main or not. If they get one of the numbers that nicks or wins the main then they win but if they throw a number that is not their main number or that is not compatible, they throw out or lose. We decided to make the game a board game just to keep track of the score and limit the playing time as the game can normally go for indefinite amounts of time. We added a timeline to the track just to further highlight the renaissance themes and while it took on a bit of a Christmas theme it was originally intended to portray a renaissance village. The chance of the game is, of course, with the dice, as with the dice games that we did at the beginning of the project, there is many different combinations and outcomes throughout the game.
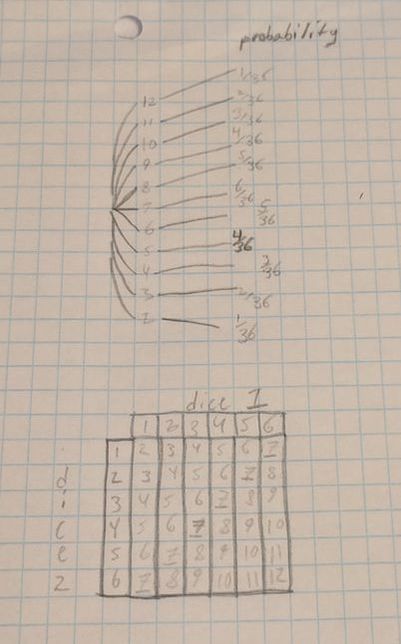
For our game we analysed which main would be statistically favorable when playing the game. We determined that the best number to choose as a main is 7 because between the two dice 7 is the number with most possible combinations. 1+6=7, 2+5=7, 3+4=7, and the reversed version of these additions for a total probability of 6/36 .
For our game we analysed which main would be statistically favorable when playing the game. We determined that the best number to choose as a main is 7 because between the two dice 7 is the number with most possible combinations. 1+6=7, 2+5=7, 3+4=7, and the reversed version of these additions for a total probability of 6/36 .
This main has high chances of showing up but the risk there is that it is more likely to throw out on a chance roll because you lose if you roll a main on a chance roll. We decided that it is still worth it to main a 7 because there will always be risks and this number increases our chances of continual winning in theory. We definitely employed Habits of Mathematicians when analyzing the probabilities of this game. We mainly looked for patterns when going through the combinations of the two dice and that is how we determined that 7 would be the best choice for a main. There are many patterns hidden in two dice rolls, for example, this is where overlapping probability can be observed, if you are looking for the chance of getting a double plus the chance of getting a 5 you will have one overlap that fix by subtracting the chance that you get a five and a double.
In all this project was very well integrated into the full Renaissance project and it was a fun way to learn about probability. There were times when the experiments felt repetitive and that we should move on to the next part of the subject but in the end I came out taking that time to really understand each thing that I was learning so I could master it and use it as we went down the road. It was certainly a lot of information to take in so I am glad that we were able to handle it all. I definitely feel that I have come out of this project knowing more about probability and I have new tools that I can use to experiment with said probability. Probability was always something that I wanted to get further into because I love the idea that you can determine the odds of something happening and I feel like I got a lot more information on how to do that.
In all this project was very well integrated into the full Renaissance project and it was a fun way to learn about probability. There were times when the experiments felt repetitive and that we should move on to the next part of the subject but in the end I came out taking that time to really understand each thing that I was learning so I could master it and use it as we went down the road. It was certainly a lot of information to take in so I am glad that we were able to handle it all. I definitely feel that I have come out of this project knowing more about probability and I have new tools that I can use to experiment with said probability. Probability was always something that I wanted to get further into because I love the idea that you can determine the odds of something happening and I feel like I got a lot more information on how to do that.